二叉树层序遍历, 你真的懂了吗？

⭐借鉴于代码随想录

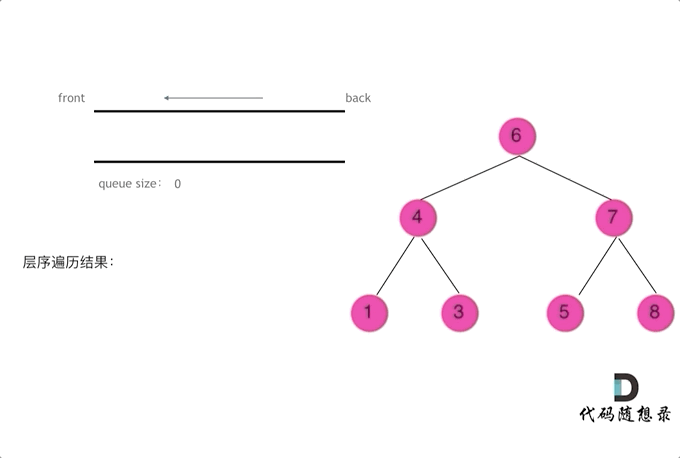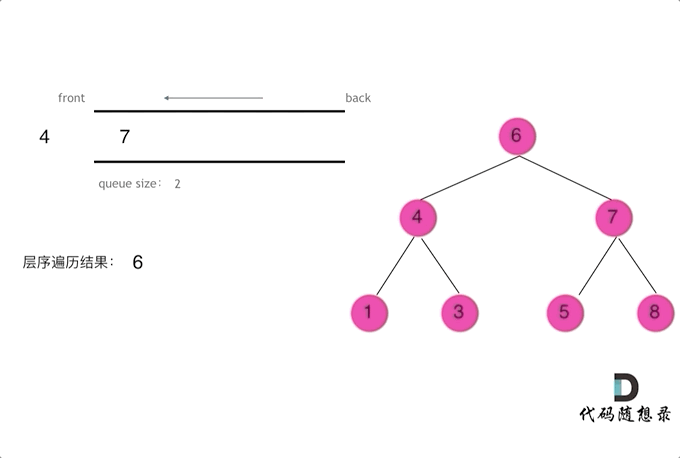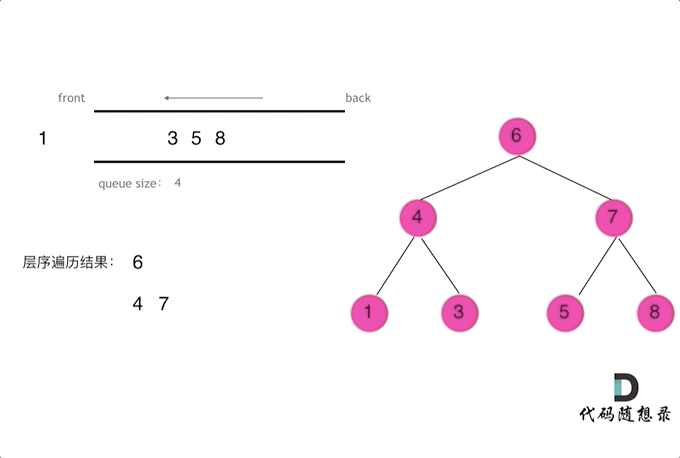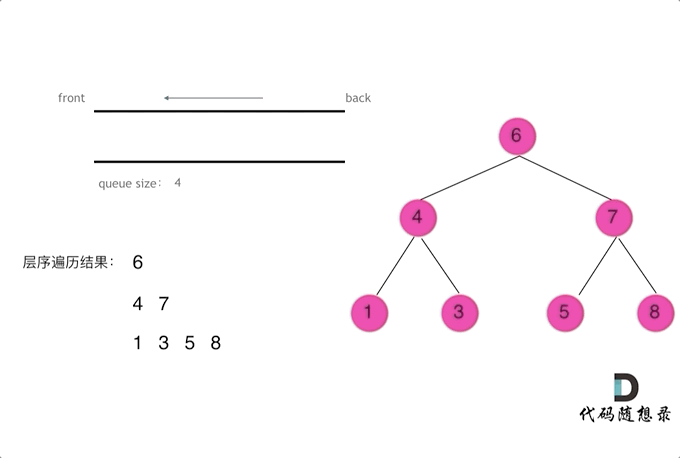
二叉树的层序遍历，就是图论中的广度优先搜索在二叉树中的应用，需要借助队列来实现

此时又发现队列的一个应用了。

来 — 一口气打十个! (其实是九个)

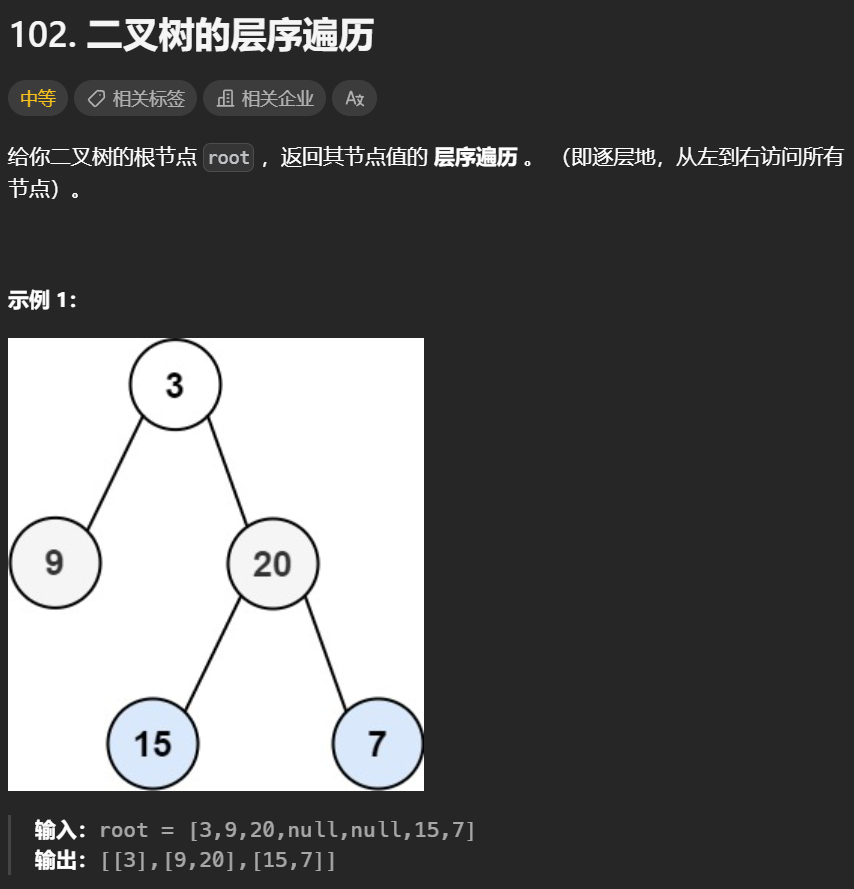
1. 二叉树的层序遍历

层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。

需要借用一个辅助数据结构即队列来实现，队列先进先出，符合一层一层遍历的逻辑，而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。

而这种层序遍历方式就是图论中的广度优先遍历，只不过我们应用在二叉树上。

使用队列实现二叉树广度优先遍历，动画如下：

var levelOrder = function(root) {
    let res = [], queue = [];
    if(root === null)  return res;
    queue.push(root); // root只是根节点
    while(queue.length) {
        let length = queue.length; // 记录当前层级有多少个节点
        let curLevel = []; // 存放每一层的所有节点
        for(let i = 0; i < length; i++) {
            let node = queue.shift(); // 每次拿到队头元素
            curLevel.push(node.val); // 存放当前层下一层的节点
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
        res.push(curLevel); //把每一层的结果(所有节点)放到结果数组
    }
    return res;
};

2. 二叉树的层序遍历(反着来)

var levelOrderBottom = function(root) {
    let res = [];
    let queue = [];
    if(root === null)return res;
    queue.push(root);
    while(queue.length) {
        let len = queue.length;
        let curLevel = [];
        for(let i = 0; i < len; i++) {
            let node = queue.shift();
            curLevel.push(node.val);
            if(node.left) queue.push(node.left);
            if(node.right) queue.push(node.right);
        }
        res.unshift(curLevel)
    }
    return res;
};

最后改一下 push 的顺序就行

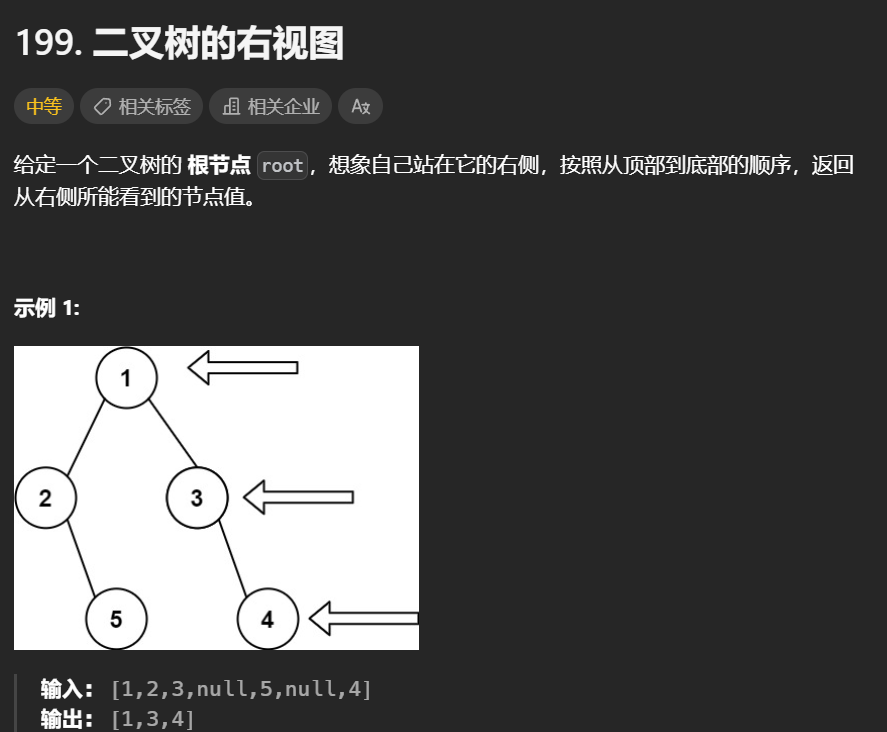
3. 二叉树的右视图

依然是按照顶部到底部的顺序, 不要搞复杂了

这里就是当遍历到每一层最右边的节点时就加入到 curLevel 数组中

var rightSideView = function(root) {
    let res = [], queue = [];
    if(!root) return res;
    queue.push(root);
    while(queue.length) {
        let len = queue.length;
        let curLevel = [];
        while(len--) {
            let node = queue.shift();
            if(!len) curLevel.push(node.val);
            if(node.left) queue.push(node.left);
            if(node.right) queue.push(node.right);
        }
        res.push(curLevel);
    }
    return res;
};

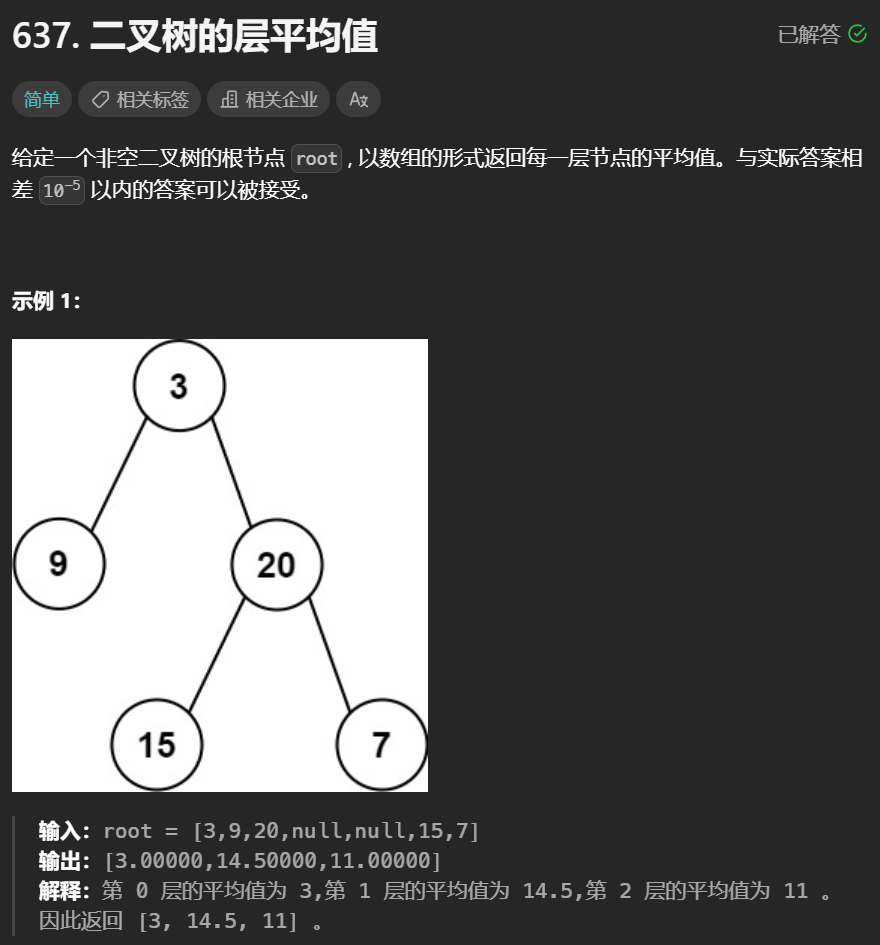
4. 二叉树的层平均值

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */

var averageOfLevels = function(root) {
    let res = [], queue = [];
    queue.push(root);
    while(queue.length) {
        let len = queue.length;
        let sum = 0;
        for(let i = 0; i < len; i++) {
            let node = queue.shift();
            sum += node.val;
            if(node.left) queue.push(node.left);
            if(node.right) queue.push(node.right);
        }
        res.push(sum / len)
    }
    return res;
};

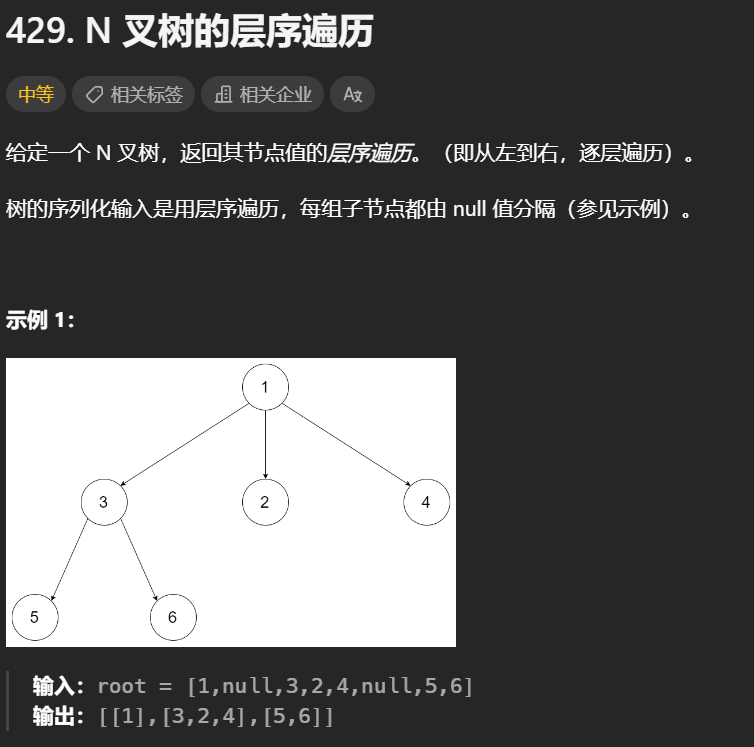
5. N 叉树的层序遍历

跟模板没啥差别

/**
 * // Definition for a Node.
 * function Node(val,children) {
 *    this.val = val;
 *    this.children = children;
 * };
 */

/**
 * @param {Node|null} root
 * @return {number[][]}
 */
var levelOrder = function(root) {
    let res = [], queue = [];
    if(root === null) return res;
    queue.push(root);
    while(queue.length) {
        let len = queue.length;
        let curLevel = [];
        for(let i = 0; i < len; i++) {
            let node = queue.shift();
            curLevel.push(node.val);
          // push所有子节点就行
            if(node.children) queue.push(...node.children)
        }
        res.push(curLevel);
    }
    return res;
};

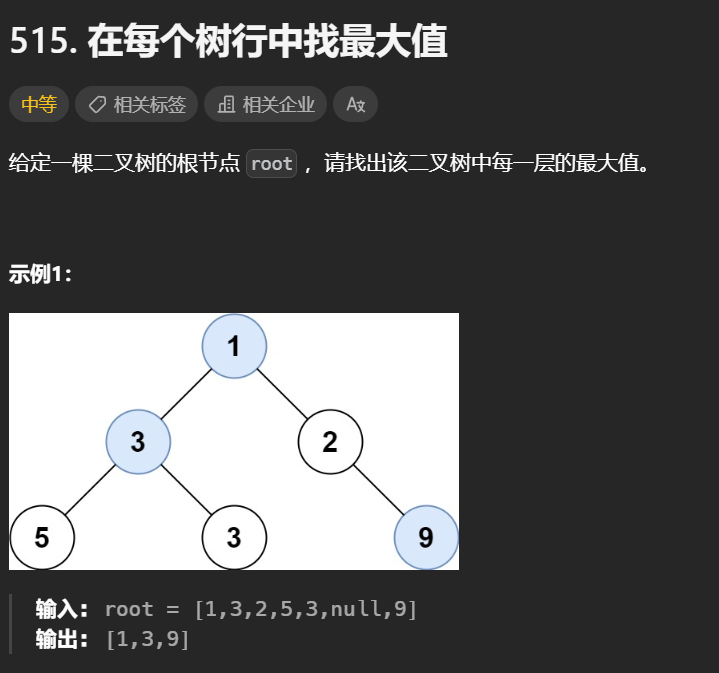
6. 在每个树行中找最大值

ar largestValues = function(root) {
    let res = [], queue = [];
    if(!root) return res;
    queue.push(root);
    while(queue.length) {
        let len = queue.length;
        let max = -Infinity;  // 注意有可能为负值, 所以不能取0
        for(let i = 0; i < len; i++) {
            let node = queue.shift();
            max = Math.max(max, node.val);
            if(node.left) queue.push(node.left);
            if(node.right) queue.push(node.right);
        }
        res.push(max);
    }
    return res;
};

7. 填充每个节点的下一个右侧节点指针

这题将 “完美二叉树” 改为 “二叉树” 也没什么区别, 一模一样的代码 ~~

/**
 * // Definition for a Node.
 * function Node(val, left, right, next) {
 *    this.val = val === undefined ? null : val;
 *    this.left = left === undefined ? null : left;
 *    this.right = right === undefined ? null : right;
 *    this.next = next === undefined ? null : next;
 * };
 */

/**
 * @param {Node} root
 * @return {Node}
 */
var connect = function(root) {
    let queue = [];
    if(root === null) return root;
    queue.push(root);
    while(queue.length) {
        let len = queue.length;
        for(let i = 0; i < len; i++) {
            let node = queue.shift();
          	// 因为前一个已经shift了, 后一个就是队首元素, 且要保证不是最后一个元素
            // 如果是最后一个元素, 正好next就等于默认的null
            if(i < len - 1) node.next = queue[0]; 
            if(node.left) queue.push(node.left)
            if(node.right) queue.push(node.right);
        }
    }
    return root;
};

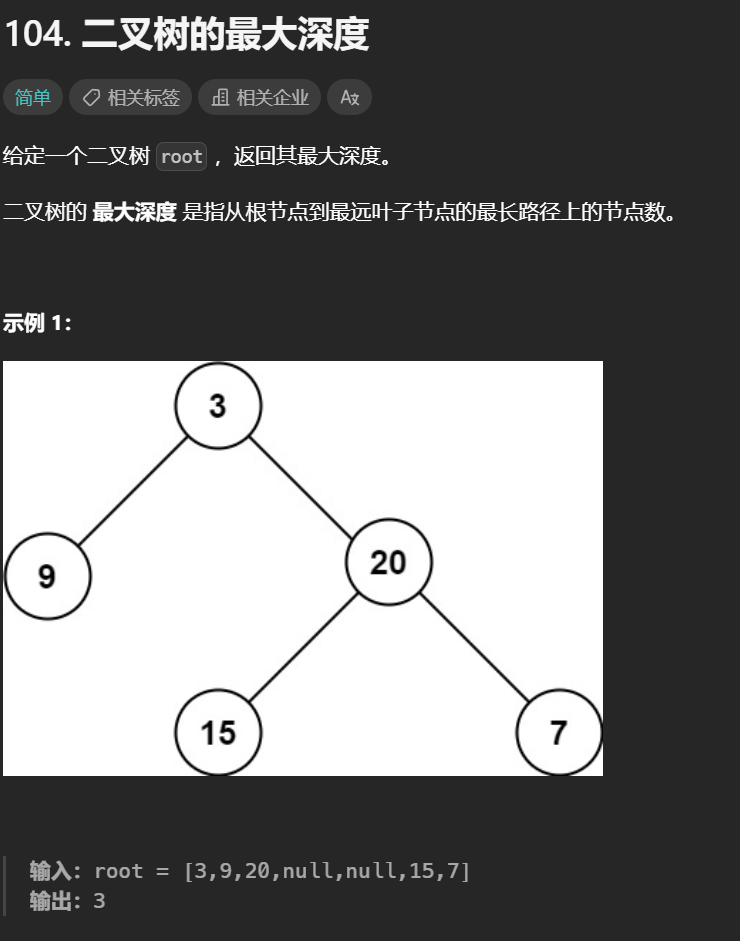
8. 二叉树的最大深度

用层序遍历也挺简单, 最大深度就是层数

var maxDepth = function(root) {
    let queue = [], cnt = 0;
    if(root === null)return 0;
    queue.push(root);
    while(queue.length) {
        let len = queue.length;
        cnt++;
        for(let i = 0; i < len; i++) {
            let node = queue.shift();
            if(node.left) queue.push(node.left);
            if(node.right) queue.push(node.right);
        }
    }
    return cnt;
};

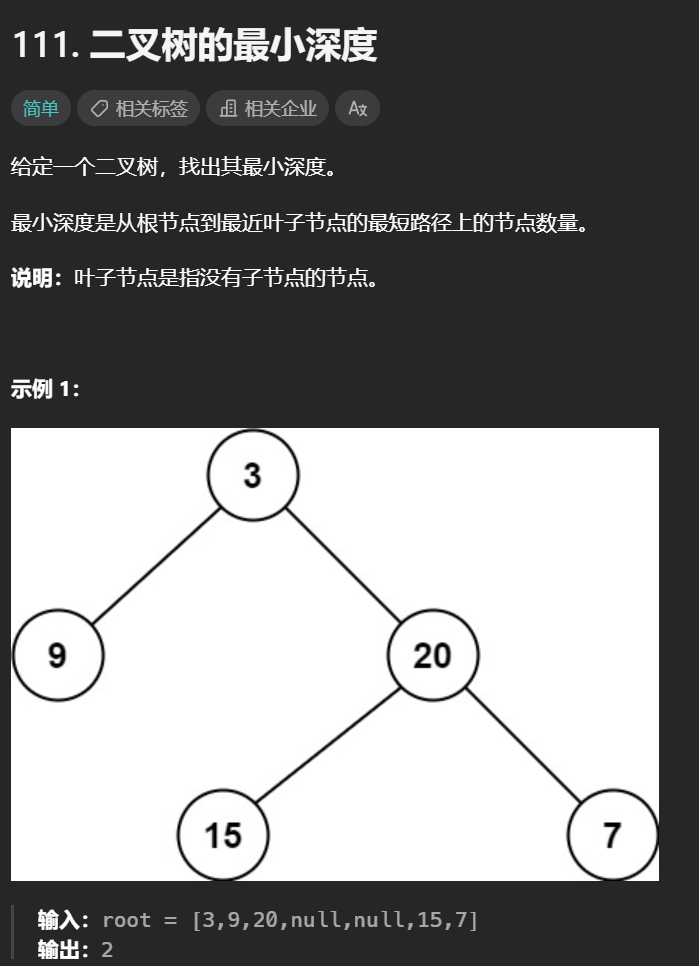
9. 二叉树的最小深度

如果某一层的节点没有左右子节点, 那么最小深度就是这一层的层数